Contents

DNA duplex stability

Introduction

The stability of the DNA double helix depends on a fine balance of interactions including hydrogen bonds between bases, hydrogen bonds between bases and surrounding water molecules, and base-stacking interactions between adjacent bases.

Slight variations in the DNA sequence can have profound implications on the stability of the DNA duplex. For example, mutations in the base sequence that result from errors that occur during DNA replication can result in mismatches that lead to relatively unstable duplexes. This instability is exploited by proofreading enzymes which recognize the mutation and replace it with the correct nucleotide (see Mutagenesis and DNA repair).

To gain an insight into DNA duplex stability, and how it is affected by changes in primary structure, scientists have studied the structure and thermodynamic stability of a variety of DNA duplexes by using a combination of physical methods including X-ray crystallography, ultraviolet (UV) melting and NMR.

Factors influencing DNA duplex stability

DNA duplex stability is determined primarily by hydrogen bonding, but base stacking also plays an important role.

Hydrogen bonding

The heterocyclic bases of single-stranded DNA have polar amino, amidino, guanidino and carbonyl groups that form a complex network of hydrogen bonds with the surrounding water molecules. Some of these bonds must be broken during duplex formation as the inter-base hydrogen bonds are formed. The overall process is one of "hydrogen bond exchange" and the net change in enthalpy upon duplex formation is partly due to ΔH (H-bonds formed) − ΔH (H-bonds broken). For duplexes of any significant length this is an exothermic process at ambient temperature. Not surprisingly the coming together of two large oligomeric molecules is entropically unfavourable ΔS is negative).

Base stacking

Inter-strand hydrogen bonding is clearly important in driving the formation of DNA duplexes, but it is by no means the only contributing factor. The individual bases form strong stacking interactions which are major contributors to duplex stability, as base stacking is much more prevalent in duplexes than in single strands (Figure 1). Base-stacking interactions are hydrophobic and electrostatic in nature, and depend on the aromaticity of the bases and their dipole moments. Base-stacking interactions in nucleic acid duplexes are partly inter-strand and partly intra-strand in nature. However, it is probably more informative to consider base pairs rather than individual bases as discrete units in order to visualize the stabilizing effects of base stacking.

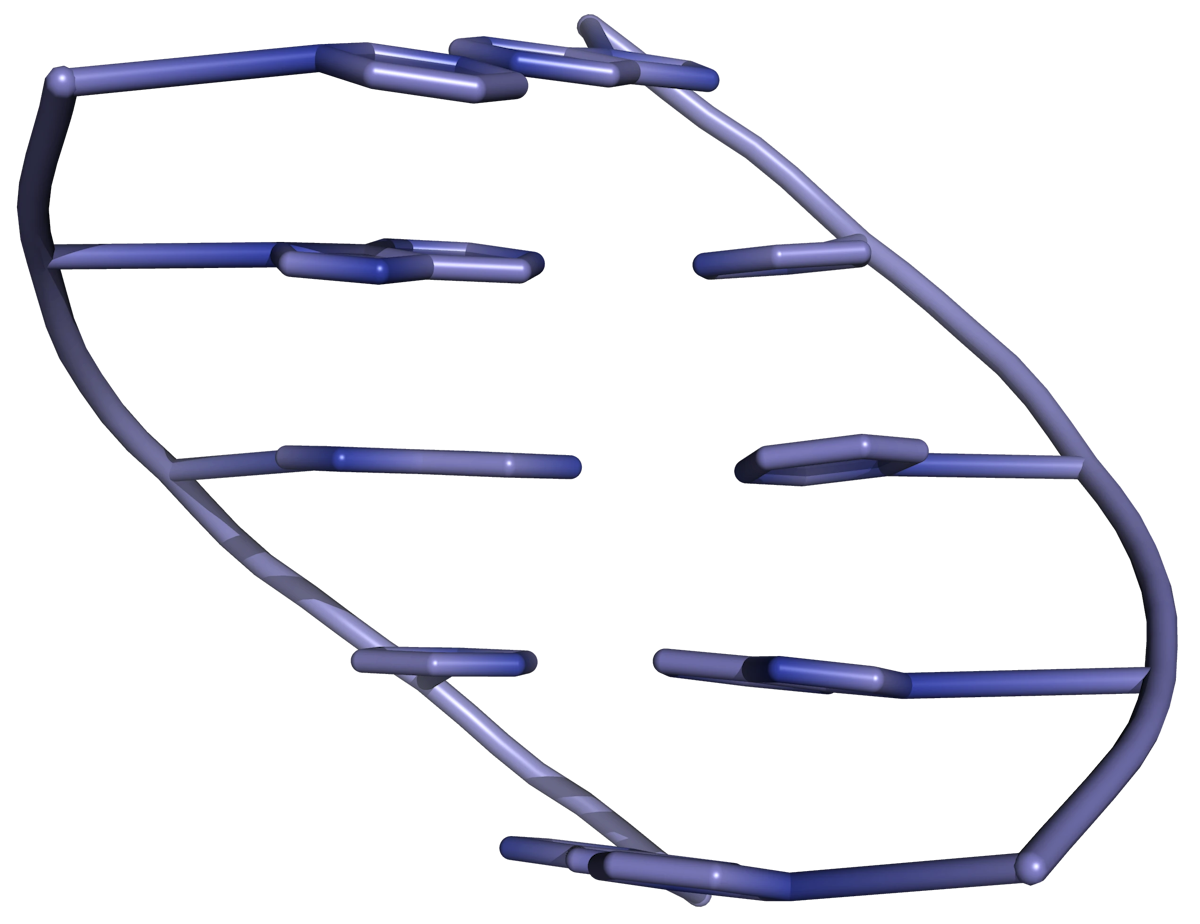
Cartoon representation of base stacking in a DNA double helix
Figure 1
Cartoon representation of base stacking in a DNA double helix

The degree of stabilization afforded by base stacking depends on the DNA sequence. Some combinations of base pairs form more stable interactions than others, so nearest neighbour base-stacking interactions are important determinants of duplex stability.

Base-stacking interactions increase with increasing salt concentration, as high salt concentrations mask the destabilizing charge repulsion between the two negatively charged phosphodiester backbones. DNA duplex stability therefore increases with increasing salt concentration. Divalent cations such as Mg2+ are more stabilizing than Na+ ions, and some metal ions bind to specific loci on the DNA duplex.

Thermodynamics of DNA duplex formation

The thermodynamic equations

ΔrG=−RTln⁡K\footnotesize\begin{equation*} \Delta_\textrm rG = -RT \ln K \end{equation*}

and

ΔrG=ΔrH−TΔrS\footnotesize\begin{equation*} \Delta_\textrm rG = \Delta_\textrm rH - T\Delta_\textrm rS \end{equation*}

can be combined to give the van 't Hoff equation by eliminating ΔrG, the change in Gibbs energy for the forward reaction (duplex formation):

−ln⁡K=ΔrHRT−ΔrSR.\footnotesize\begin{equation*} - \ln K = \frac{\Delta_\textrm rH}{RT} - \frac{\Delta_\textrm rS}{R}. \end{equation*}

This can be rearranged to give

1T=−RΔrHln⁡K+ΔrSΔrH,\footnotesize\begin{equation*} \frac{1}{T} = -\frac{R}{\Delta_\textrm rH} \ln K + \frac{\Delta\textrm rS}{\Delta_\textrm rH}, \end{equation*}

in which ΔrH is the enthalpy change, ΔrS is the entropy change, R\footnotesize R is the gas constant and K\footnotesize K is the equilibrium constant. K\footnotesize K can be expressed as a function of the extent of association, α\footnotesize\alpha, and of the initial concentration of single-stranded DNA. This is described below for three different hybridization scenarios.

Standard DNA

When two complementary (but not self-complementary) strands of DNA are mixed in solution, an equilibrium is rapidly established between the single strands, A and B, and the (double-stranded) duplex, C:

\ceA+B<=>C\footnotesize\ce{A + B <=> C}

Assuming equal initial concentrations for A and B ([A]0=[B]0)\footnotesize{([A]_0 = [B]_0}) and no C formed ([C]0=0)\footnotesize{([C]_0=0)}, at equilibrium,

K=[C]eq[A]eq[B]eq=α[A]0(1−α)[A]0(1−α)[B]0)=α(1−α)2[A]0.\footnotesize\begin{equation*} K = \frac{[\textrm C]_\textrm{eq}}{[\textrm A]_\textrm{eq}[\textrm B]_\textrm{eq}} = \frac{\alpha[A]_0}{(1-\alpha)[A]_0(1-\alpha)[B]_0)} = \frac{\alpha}{(1-\alpha)^2[A]_0}. \end{equation*}

At the midpoint of the melting curve, α=12\footnotesize{\alpha=\frac{1}{2}}, so

K=1214[A]0=2[A]0\footnotesize{K = \frac{\frac{1}{2}}{\frac{1}{4}[A]_0} = \frac{2}{[A]_0}}

and

−ln⁡K=−ln⁡(2[A]0)=ln⁡([A]02).\footnotesize\begin{equation*} -\ln K = -\ln\left(\frac{2}{[A]_0}\right) = \ln\left(\frac{[A]_0}{2}\right). \end{equation*}

Reverse-complementary DNA

For reverse-complementary DNA, two single-stranded DNA molecules of the same species can hybridize with each other, and an equilbrium is established in solution between single-stranded and double-stranded DNA as follows:

\ce2A<=>C\footnotesize\ce{2A <=> C}

As with the case above, the equilibrium constant K\footnotesize K can be written as a function of the extent of association, α\footnotesize\alpha, and of the initial concentration of single-stranded DNA, [A]0\footnotesize{[A]_0}. At equilibrium,

K=[C]eq[A]eq2=12α[A]0(1−α)2[A]02=α2(1−α)2[A]0.\footnotesize{K = \frac{[\textrm C]_\textrm{eq}}{{[\textrm A]_\textrm{eq}}^2} = \frac{\frac{1}{2}\alpha [\textrm A]_0}{(1-\alpha)^2{[\textrm A]_0}^2} = \frac{\alpha}{2 (1-\alpha)^2[\textrm A]_0}}.

At the midpoint of the melting curve, α=12\footnotesize{\alpha = \frac{1}{2}}, so K=1[A]0\footnotesize{K = \frac{1}{[A]_0}} and −ln⁡K=−ln⁡(1[A]0)=ln⁡([A]0)\footnotesize{-\ln K = -\ln \left(\frac{1}{[A]_0}\right) = \ln \left([A]_0\right)}.

Self-complementary DNA

Self-complementary DNA molecules can undergo intramolecular hybridization, for example to form hairpin loops, resulting in an equilibrium

A ⇌ C.

At equilibrium,

K=[C]eq[A]eq=α[A]0(1−α)[A]0.\footnotesize\begin{equation*} K = \frac{[\textrm C]_\textrm{eq}}{[\textrm A]_\textrm{eq}} = \frac{\alpha [A]_0}{(1-\alpha)[\textrm A]_0}. \end{equation*}

At the midpoint of the melting curve, α=12\footnotesize{\alpha = \frac{1}{2}}, so K=1\footnotesize{K = 1} and −ln⁡K=0\footnotesize{-\ln K = 0}.

Inserting this expression into the van 't Hoff equation (see below for the standard case) shows that the melting temperature does not depend on the concentration, which is to be expected from an intramolecular reaction.

Experimental determination of DNA duplex stability

UV melting

Heating double stranded nucleic acids causes the strands to unwind (denature) by disrupting the ordered stacking of the bases and breaking hydrogen bonds. The process can be conveniently monitored by an increase in UV absorbance as the double strands unwind to single strands (owing to hypochromicity). The thermal denaturation of double-stranded DNA is progressive and the concerted melting of the whole structure occurs at a well-defined temperature, corresponding to the mid-point of a smooth transition. This temperature is known as the melting temperature (Tm).

The example in Figure 2 shows a melting curve (UV absorption as a function of temperature). Slow heating of double-stranded DNA causes the unwinding of the ordered helical structure into the two single-stranded constituents. This can be seen as a sigmoidal curve of increasing UV absorption. The mid-point, corresponding to the precise melting temperature (Tm) of the duplex, is indicated.

UV melting curve of a DNA duplex
Figure 2
UV melting curve of a DNA duplex

To determine thermodynamic parameters, samples are made up at different concentrations, each containing equal amounts of two complementary sequences of DNA (A and B) in a salt/buffer solution. On mixing at ambient temperature the two strands of DNA spontaneously form a duplex (C) (i.e. α=1\footnotesize{\alpha = 1}) (this is true for DNA strands of any reasonable length). Each sample is heated in a UV spectrometer from 20 °C to (say) 80 °C at a rate of one degree per minute and the absorbance is monitored as shown in Figure 2. The melting temperature, Tm, is the temperature at the maximum absorbance gradient dAdT\footnotesize{\frac{\textrm dA}{\textrm dT}} and corresponds to 50% association (α=12\footnotesize{\alpha = \frac{1}{2}}). The graph (Figure 3) shows the relationship between absorbance and concentration and illustrates the slight increase in Tm with increasing DNA concentration.

UV melting curve of an DNA duplex at different concentrations
Figure 3
UV melting curve of an DNA duplex at different concentrations

With α=12\footnotesize{\alpha = \frac{1}{2}}, using Eqn. (6), Eqn. (4) becomes

1Tm=RΔrHln⁡([A]02)+ΔrSΔrH.\footnotesize\begin{equation*} \frac{1}{T_\textrm m} = \frac{R}{\Delta_\textrm rH} \ln \left(\frac{[A]_0}{2}\right) + \frac{\Delta_\textrm rS}{\Delta_\textrm rH}. \end{equation*}

A graph of 1/Tm against ln⁡([A]02)\footnotesize{\ln\left(\frac{[\textrm A]_0}{2}\right)} therefore has a gradient RΔrH\footnotesize{\frac{R}{\Delta_\textrm rH}} and an intercept ΔrSΔrH\footnotesize{\frac{\Delta_\textrm rS}{\Delta_\textrm rH}} (neglecting the temperature-dependence of ΔrS and ΔrH). The reciprocals of the recorded Tm values are plotted against the ln⁡([A]02)\footnotesize{\ln\left(\frac{[\textrm A]_0}{2}\right)} values and linear regression is used to determine ΔrH and ΔrS. Finally, ΔrG is evaluated. Figure 4 shows such a van 't Hoff plot:

Van 't Hoff plot for the duplex dGGCTATCTATCTGC-dGCAGATATATAGCC (containing a C-T mismatch) giving \footnotesize{\Delta_\textrm rH = -339.1~\textrm{kJ mol}^{-1}}, \footnotesize{\Delta_\textrm rS = -1~\textrm{J K}^{-1} \textrm{mol}^{-1}} and \footnotesize{\Delta_\textrm rG = -338.9~\textrm{kJ mol}^{-1}} (at 298 K).
Figure 4
Van 't Hoff plot for the duplex dGGCTATCTATCTGC-dGCAGATATATAGCC (containing a C-T mismatch) giving ΔrH=−339.1 kJ mol−1\footnotesize{\Delta_\textrm rH = -339.1~\textrm{kJ mol}^{-1}}, ΔrS=−1 J K−1mol−1\footnotesize{\Delta_\textrm rS = -1~\textrm{J K}^{-1} \textrm{mol}^{-1}} and ΔrG=−338.9 kJ mol−1\footnotesize{\Delta_\textrm rG = -338.9~\textrm{kJ mol}^{-1}} (at 298 K).

Calorimetry

Calorimetry is a classically important method for measuring DNA duplex stability, although UV melting has proved more popular owing to the availability of UV spectrometers with temperature-controlled sample chambers, and the relative ease of recording Tm values. Whereas UV melting provides an indirect method for measuring ΔrH, ΔrS and ΔrG for melting, calorimetry allows more direct measurement of these thermodynamic parameters.

Prediction of DNA duplex stability

The melting temperature (Tm) of a DNA duplex and the effect of salt can be predicted using the formula [1-2]

Tm=(81.5+16.6log⁡10([Na+])+41(nG+nC)nA+nG+nC+nT−675nA+nG+nC+nT)°C,\footnotesize\begin{equation*} T_\textrm m = \left(81.5 + 16.6\log_{10}([\textrm{Na}^+]) + \frac{41(n_\textrm G + n_\textrm C)}{n_\textrm A + n_\textrm G + n_\textrm C + n_\textrm T} - \frac{675}{n_\textrm A + n_\textrm G + n_\textrm C + n_\textrm T}\right)\degree\textrm C, \end{equation*}

where ni\footnotesize{n_i} is the number of bases of type i\footnotesize i present. However, this formula only applies to DNA duplexes containing exclusively Watson-Crick A.T and G.C base pairs under a well-defined set of conditions, and cannot be used to determine the melting temperatures of mismatch-containing duplexes.

Tuning DNA duplex stability

When designing and synthesizing synthetic DNA oligonucleotides, for example for use in antisense therapy or as PCR probes, it is often desirable to either increase or decrease the stability of the duplex formed on binding to complementary DNA.

Nucleic acid analogues

Artificial nucleic acid analogues bind to complementary DNA. Peptide nucleic acid (PNA) , a neutral molecule, forms particularly strong and specific interactions with DNA. Stretches of PNA can be incorporated into DNA oligonucleotides to increase duplex stability; but care must be taken in desigining the PNA-DNA junction, and the stablizing effect of the PNA can be offset by the destabilizing impact of the junction. Locked nucleic acid (LNA) and unlocked nucleic acid (UNA) are analogues of RNA that can be easily incorporated into DNA oligonucleotides during solid-phase oligonucleotide synthesis, and respectively increase and decrease duplex stability. LNA and UNA phosphoramidite monomers are not readily available, however, and it is not always easy to predict the effect of incorporating LNA and UNA units into DNA oligonucleotides before they are synthesized.

Modified bases

Modified DNA bases that increase the stability of base pairs (and therefore the duplex as a whole) have been developed. These modified bases can be incorporated into oligonucleotides during solid-phase synthesis and offer a more predictable method of increasing DNA duplex stability.

AP-dC (G-clamp)

AP-dC (G-clamp) is a tricyclic analogue of cytosine. Like cytosine, G-clamp forms base pairs with guanine; but, while G·C base pairs are stabilized by three hydrogen bonds, G·G-clamp base pairs have four hydrogen bonds (Figure 5). The extra hydrogen bond can lead to an increase in Tm of 18 °C. The incorporation of multiple G-clamp bases can result in further increases in duplex stability.

Structure of the G·G-clamp base pair G·G-clamp base pairs (right) increase the stability of a DNA duplex by up to 18 °C relative to G·C base pairs (left).
Figure 5
Structure of the G·G-clamp base pair G·G-clamp base pairs (right) increase the stability of a DNA duplex by up to 18 °C relative to G·C base pairs (left).

2-Aminoadenine

2-Aminoadenine forms base pairs with thymine that are stabilized by three hydrogen bonds (one more than the two hydrogen bonds of A·T base pairs) (Figure 6). Each substitution of an A·T base pair by a 2-aminoadenine·thymine base pair increases the stability of the duplex by about 3 °C.

Structure of the 2-aminoadenine·thymine base pair 2-aminoadenine·thymine base pairs (right) increase the stability of a DNA duplex by around 3 °C (per substitution) relative to A·T base pairs (left).
Figure 6
Structure of the 2-aminoadenine·thymine base pair 2-aminoadenine·thymine base pairs (right) increase the stability of a DNA duplex by around 3 °C (per substitution) relative to A·T base pairs (left).

Other modified bases

Modest increases in duplex stability have been observed with other modified bases, including 5-methylcytosine and C(5)-propynylcytosine (replacing cytosine), and C(5)-propynyluracil (replacing thymine).

[1] Howley et al., J. Biol. Chem. 1979, 254, 11, 4876.

[2] Baldino et al., Methods Enzymol. 168, 761-77, 1989.